ひとり勉強会

ひとり楽しく勉強会

Coqの入門記事を書く会 (2)

Coq

第２回です。前回は「forall」と「->」の扱い方でした。今回は、「ならば (->)」以外の定番の論理演算、「and」「or」「not」のお話です。

実は、Coq の本当に言語組み込みの命題構成子は forall と -> だけで、「and」「or」「not」は、Coq使いなら自分で同じ機能のものを簡単に作れてしまう「ユーザー定義命題」です（もちろん、共通のものがないと不便なので標準ライブラリで真っ先に定義されてますけど）。逆に言うと、もっと本格的なCoqコードで出てくる複雑そうな命題も、全部、「and」「or」「not」と同じユーザー定義型の仕組みで定義されてますので、「and」「or」「not」の扱いさえマスターすれば、他のどんなユーザー定義の命題の証明も同じ道具で書けちゃいますよ。

andとorとnot: ド・モルガン (2.1)

Coq

andとorとnotを分けて説明するのが面倒くさいので、いきなり全部入りの定理を例にしましょう。今回のお題はド・モルガンの法則です。

Lemma De_Morgan:
  forall A B: Prop, ~(A \/ B) -> (~A /\ ~B).
Proof.

「(AまたはB)ではない、ならば、(Aではない、かつ、Bではない）」です。∨ が「または」で、∧ が「かつ」で、「~」が否定の「ではない」です。∨と∧はバックスラッシュを使って書くので、フォント環境によっては円記号に見えてしまっているかも。その場合はすみません、心眼で￥を＼と読んで下さい。

そういえば前回は Theorem Modus_ponens と "Theorem" (定理) で書き始めましたが、今回は "Lemma" (補題) です。Coq 的には違いは何もありません。趣味の問題です。"Proposition" (命題) や "Corollary" (系)、"Fact"、"Remark" など色々ありますが趣味で使い分けて下さい。

notの扱い

さて、まず、否定の ~A は、「A -> False」の省略形です。リファレンスから引用します。Coq.Init.Logic.not:

Definition not (A:Prop) := A -> False.
Notation "~ x" := (not x) : type_scope.

「Aではない」とはすなわち、「Aならば偽」「Aだと仮定すると矛盾が生じる」である。これがCoqでの、そしてCoqがベースにしている論理体系での「~」の定義であります。False の定義はあとで解説しますが、とりあえず単にそういう名前の命題と思っておいて下さい。

「ならば」の扱いなら前回やって慣れてますので、安心ですね。「"not" なんて見慣れない単語を使わないで、全部 "->" の言葉でしゃべってください」と Coq さんに伝えましょう。

  unfold not.

"unfold" tactic を使います。単に、Definition ... := で定義された定義をインライン展開するだけのtacticです。

ついでに intros. しておきました。

andの扱い

示さないといけないゴールの形が、(A→False)∧(B→False) になりました。この ∧ とは何者かというと… Coq.Init.Logic.and:

Inductive and (A B:Prop) : Prop :=
  conj : A -> B -> A /\ B

where "A /\ B" := (and A B) : type_scope.

こんな物体です。なにやら複雑ですが、とりあえず最後の１行は「"A∧B" という中置演算みたいな記法は、(and A B) の略記です」と言ってるだけです。本体は上２行。"Inductive" 宣言を使って、二つのことを宣言しています。

  • "A∧B" という新種の命題をこれから使います！
  • この "A∧B" の「公理」は A -> B -> A∧B です！

"A∧B"が成り立つのは、Aが成り立って、しかもBが成り立っているとき、その時に限ります。つまり "Aならば(Bならば(A∧B))" が無条件で成立する…そういう∧という命題を使って色々書いたり証明したりするんでよろしくお願いします、とCoqさんに伝えるのがInductive宣言です。

さてさて、定義の話はいいから、証明のやり方はどうするのでしょうか。

実は、もう我々は証明のしかたを知っています。

  • ゴールは hoge ∧ fuga という形です
  • conj : hoge -> fuga -> hoge ∧ fuga という公理があります

公理はいつでも無条件に使えるので、仮定と同じように、apply することができて…

 apply conj.

"(A->False) ∧ (B->False)" を示すためには、A->False を示して、B->False を示せば、後は conj を使えば証明できます。そういう感じで証明しますんでよろしく、とCoqさんに伝えると

二つのゴールができました。

orの扱い

続いて、一つ目のゴールは "A->False" です。ゴールが "->" の形なので、何も考えず

  intros.

するとゴールが "False" になりますが、仮定を眺めると False を作れるのは "H: A∨B->False" しかないので、これをapplyしておきます。

 apply H.


ゴールは "A∨B" になりました。さてどうしましょう。定義を見ると Coq.Init.Logic.or:

Inductive or (A B:Prop) : Prop :=
  | or_introl : A -> A \/ B
  | or_intror : B -> A \/ B

where "A \/ B" := (or A B) : type_scope.

今度は、公理が２つあります。

  • or_introl: "A"が成り立つなら、"AまたはB"が成り立つ
  • or_intror: "B"が成り立つなら、"AまたはB"が成り立つ

まあor(または)の意味として納得の行く定義です。

というわけで、ゴールを証明するには "apply or_introl." か "apply or_intror." を使えばよいのですが…どっちが正解でしょうか？

  • ゴール A∨B に、or_introl: A->(A∨B) を apply すると、新ゴールは A になります
  • ゴール A∨B に、or_intror: B->(A∨B) を apply すると、新ゴールは B になります

どっちなら続きを証明できるかというと、今回は仮定に "H0: A" があるので、新ゴール A なら"exact H0."で証明完了です。というわけで、or_introl の方を使います。

  apply or_introl.
  exact H0.

こういう風に、or のような分岐があると「どっちに行ったら証明できるか」をよく考えて選んでやる必要があります。証明の完全な機械化は難しくて、Coqのように人間が考えて証明記述してやるシステムが必要な理由の一端は、ここにあります。頑張って人類の発想力を発揮しましょう。

apply conj でできたもう一つのゴール "B->False" も、同じように証明できます。こっちは or_intror の方を使います。

  intros.
  apply H.
  apply or_intror.
  exact H0.
Qed.

証明完了！

andとorとnot: カリーハワード (2.2)

Coq

「プログラミング言語としてみると」さっきの証明は何をやっていたことになるんでしょう。

"Inductive"は、ユーザー定義の新しい命題を定義するのでした。そして、命題＝型です。つまり、ユーザー定義の新しい型を作る機能が対応します。Haskell だと "data" ですね。

data And a b = 
 Conj a b

data Or a b =
   OrIntroL a
 | OrIntroR b

Inductiveによるandとorの定義をHaskellで書き直すと、↑こうなります。公理とは、要するにコンストラクタです。はい。

class And<A,B> {
  public And(A a, B b) { ... }
}

class Or<A,B> {
  public Or(A a) { ... }
  public Or(B b) { ... }
}

Javaで書くとこんな感じです。Andは、2引数のコンストラクタを1つ持つ型です。Orは、1引数のコンストラクタが2つ。どっちを使っても作れますが、どっちかを使わないと作れません。

ちなみに False は、Coq.init.Logic.False:

Inductive False : Prop :=.

公理が一つもない…つまり証明する手段が１つも用意されていない命題、それがFalse、という定義です。Haskellでも

{-# OPTIONS_GHC -XEmptyDataDecls #-}
data False

こう、こういう変な型を定義するには追加オプションが要りますけど、作れます。

さて、あらためて、ド・モルガンの証明とはなんだったかというと…

de_morgan :: (Or a b -> False) -> And (a -> False) (b -> False)

Haskellで「この型を持つ値を作ってね！なんでもいいから！」と言われたら、どうしますか？

de_morgan f =
 Conj (\x -> f (OrIntroL x)) (\y -> f (OrIntroR y))

たとえば、こんな風に書けますね。これが、さっきCoqで作った証明です。

andとorとnot: コンストラクタ (2.3)

Coq

ここまでの内容をまとめると、

  • ゴールが A∧B の形なら ∧の公理(コンストラクタ)を使う
    • つまり apply conj.
  • ゴールが A∨B の形なら ∨の公理(コンストラクタ)を使う
    • つまり apply or_introl.
    • または apply or_intror.
    • どっちがいいかは人間が頑張って考える。

です。

これはこれでいいんですけど、「∧のコンストラクタの名前ってなんだったけ…」「∨のコンストラクタって…」って毎回思い出したり、リファレンス引いたりするのは面倒ですよね。

この辺は、自動化してくれる tactic があります。

Lemma De_Morgan:
  forall A B: Prop, ~(A \/ B) -> (~A /\ ~B).
Proof.
  unfold not.
  intros.
  constructor.  (* apply conj. の代わり *)

constructor. と打つと、名前忘れたけどコンストラクタ使うぜ！という意味になって、Coqさんが上手いことやってくれます。
orの場合はコンストラクタが2つあるので…

  intros.
  apply H.
  constructor 1. (* apply or_introl. の代わり *)
  exact H0.

  intros.
  apply H.
  constructor 2. (* apply or_intror. の代わり *)
  exact H0.
Qed.

どっちのコンストラクタなのか、「1番目のやつ！」「2番目のやつ！」と指定してあげましょう。番号指定しないと、コンストラクタを先頭から順にapplyしてみて成功した最初の結果を返すみたいです。

実は、さらにさらに、短く書く略記tacticも用意されています。

constructor.
ゴール命題の、コンストラクタをapply。(複数ある場合は最初にマッチした物)
constructor n.
ゴール命題の、n番目のコンストラクタをapply
split.
1つしかコンストラクタがないゴールに。そのコンストラクタをapply
left.
丁度2つコンストラクタがあるゴールに。constructor 1 と同じ
right.
丁度2つコンストラクタがあるゴールに。constructor 2 と同じ
splitは「"A∧B"を証明」というゴールを「Aを証明」と「Bを証明」に分ける(split)感覚で、leftは「"A∨B"を証明」というゴールを「Aを証明」に左(left)だけ残して変える感覚ですかね。rightは右。constructorのただの別名なので、splitもleftもrightも、andやor以外にも使えます（かえって意味がわかりにくくなったりするかもしれませんが…）。

andとorとnot: デストラクト (2.4)

Coq

「コンストラクタがあるならデストラクタはないんですか」

あるのです。これを語らなくては話が終わりません。コンストラクタの逆の話なので、例題も逆にしましょう。ド・モルガンの法則は逆向きにも成り立ちます。

Lemma De_Morgan2:
 forall A B: Prop, (~A /\ ~B) -> ~(A \/ B).
Proof.
 unfold not.
 intros.

とりあえず unfold と intros してみるのは良いとして…

次、どうしましょう。仮定にあるのは

  • H: (A->False)∧(B->False)
  • H0: A∨B

だけで、-> がないので、もう apply もできません。困った。

逆に考えるんだ。

  • 「∧を証明できるのは公理 conj: hoge→fuga→hoge∧fuga しか存在しない」
  • 既に仮定 H に「(A->False)∧(B->False)」がある
  • これは conj に「A->False」と「B->False」を渡して作ったとしか考えられない

なので、「(A->False)∧(B->False)」を仮定しても良いなら、同時に、「A->False」と「B->False」も既に成り立っていると仮定して良いでしょう！

と Coq さんに伝えるのが、destruct という tactic です。

 destruct H.

仮定から∧が消えて

  • H: A->False
  • H1: B->False
  • H0: A∨B

こう分解されます。「A∧Bを仮定してCが証明できる」ことを示すには、「AとBを仮定してCが証明できる」ことを示せば十分、と仮定を分解するのがdestructです。

もう一個、仮定に、分解できそうな子がいますね。

  • 「∨を証明できるのはor_introlかor_introrのどちらかしかない」
  • 既に仮定に H0: A∨B がある。これは
    • 「or_introl に A を渡して作った」か
    • 「or_intror に B を渡して作った」のどっちかしかあり得ない。

どっちかわからないけど、両方の場合を考えてどっちもゴールが証明できたらOKじゃない？とCoqさんにお願い。

 destruct H0.


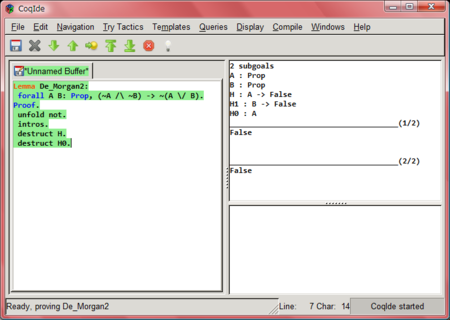
「A∨Bを仮定してCが証明できる」ことを示すには、「Aを仮定してCが証明できる」と「Bを仮定してCが証明できる」の二つのゴールを証明すればよいのです。というわけでゴールが２つにわかれます。

ここまで来れば簡単ですね。

 exact (H H0).
 exact (H1 H0).
Qed.

まとめると…

Inductiveでユーザー定義した命題の公理（conj や or_introl や or_intror）は、「それを使うとユーザー定義命題を証明できる」という意味と、「それ以外の方法では決して証明できない」という、２つの意味があります。前者の性質を使うのがコンストラクタによる証明で、後者を使うのがdestruct tacticによる証明です。

destruct H.
仮定Hの型TがInductiveで、そのコンストラクタが A->B->T、C->D->T、E->F->T、… だったら、「Hを仮定してゴールを示す」という状態を「AとBを仮定してゴールを示す」「CとDを仮定してゴールを示す」「EとFを仮定してゴールを示す」…に分解する
destruct H as [HA HB].
destruct H as [HA|HB].
destruct H as [HA [HB HC] ].
説明してませんでしたが、destructした時に新しく増える命題にはasで名前をつけることができます。andのようにゴールが分岐せず仮定が増える部分には[HA HB]と並べ、orのようにゴールが増える部分には[HA|HB]と並べます。ネストさせるとA∧B∧Cみたいなのを一気にdestructしたりできます。詳しくはリファレンスをどうぞ。
decompose [and or] H.
実はわたしは使ったこともちゃんと調べたこともないのですけど、賢く全部destructしつくしてくれる感じのtactic？
elim H
case H
destruct よりももっとプリミティブな操作です。destructすると「元々あった仮定を消して新しく分解後の仮定を追加」しますが、elim を使うと「元々の仮定は消さない。分解後の結果は過程に追加するのではなく、ゴールに->で追加」します。さらに、「分解した仮定Hが他の仮定の中に使われていた場合にそのHも書き換える」がdestructで書き換えないのがelim。まあなんだかややこしいのですが、要は、「destructはちょっとやり過ぎで困る」と思ったらelimに変えて試してみるといいかも…。
まあ、ややこしいことは気にせず仮定にInductiveなものがあったらとりあえずdestructしてみるという証明戦略は結構うまくいく気がします。

ややこしいことは気にせずといえば、カリーハワード対応脳の人には、destructのもっとずっとわかりやすい説明があります。要するにこれは、

Print De_Morgan2.

De_Morgan2 =
fun (A B : Prop) (H : (A -> False) /\ (B -> False)) (H0 : A \/ B) =>
match H with
| conj H1 H2 =>
    match H0 with
    | or_introl H3 => H1 H3
    | or_intror H3 => H2 H3
    end
end

パターンマッチなのです。

andとorとnot以外のInductive (2.5)

Coq

何度か繰り返しているように、andやorやFalseは、Coqに組み込みの摩訶不思議な何かではなく、ユーザー定義できる命題です。andやorに使える証明方法は、他のInductive命題にもそのまま使えます。試しに他に何か自作してみましょう。

こんなの考えてみました。

Inductive major (A B C:Prop) : Prop :=
| ab : A->B->major A B C
| bc : B->C->major A B C
| ca : C->A->major A B C.

AとBとCのうち、2個以上が成り立つなら成り立つ、多数決命題 major A B C を定義しました。例えば、こんな定理が成り立ちます。

Theorem majmaj:
 forall A B C: Prop,
   major A B C -> ~major (~A) (~B) (~C).
Proof.

とりあえず unfold not. して、intros. して…あとは仮定に major ばっかりになるので、Inductive な命題が仮定にあるときは…？ 練習問題です(^^)。


他に重要な例としては、Anarchy Proof の問題でも時々でてきます（Prime is decidable など）が、{A}+{B} というのがあります。これの定義はCoq.Init.Specif.sumbool:

Inductive sumbool (A B:Prop) : Set :=
  | left : A -> {A} + {B}
  | right : B -> {A} + {B} 
 where "{ A } + { B }" := (sumbool A B) : type_scope.

コンストラクタの名前が違うだけで、ほとんど A∨B と同じです。実際、∨を{}+{}に変えた

Lemma De_Morgan3:
 forall A B: Prop,
  ({A}+{B}->False) -> ((A->False) /\ (B->False)).

でも

Lemma De_Morgan4:
 forall A B: Prop,
  ((A->False) /\ (B->False)) -> ({A}+{B}->False).

でも、全く同じに、"constructor" と "destruct" を使って証明できます。試してみて下さい。練習問題です(^^)。こんな風に、見たことのない新しい命題が現れても、どれもandやorと同じく、constructorとdestructで証明にとりかかれます。簡単ですね。


※ {A}+{B} に関しては、A∨B と唯一違うところは、∨の方は:Propと宣言されてましたが、{}+}{}の方は:Setと宣言されているところです。PropとSetの違いはそのうち多分説明するような気がしますが、とりあえず証明を考える際に問題となる違いは１点だけ。

  • ゴールが Set のときは、Prop の destruct はできない

この制約のせいで、"forall A B:Prop, {A}+{B} -> A\/ B" は証明できますが、"forall A B:Prop, A\/ B -> {A}+{B}" はできません。この形になってしまったときは、destructを使わずになんとか迂回して証明することになります。

andとorとnot: 次回予告 (2.6)

Coq

もう今回の内容でInductiveの扱いは完璧…！

といいたいところなんですが、「再帰的なInductive」の証明テクニックの解説が実はまだ残っています。次は多分それについて書きたいなあと思っています。それかFalse周りの証明をさらにいろいろ。