ひとり勉強会

ひとり楽しく勉強会

VSTTE 2012 Software Verification Competition

Coq

VSTTEという国際会議の開催した「ソフトウェア検証大会」

に挑戦していました。48時間で5問の仕様と実装が提示されて、その正しさ、つまり停止性や、配列の範囲外アクセスをしないこと、仕様を満たしていることなどを、なんでも自由なツールを使っていいから検証してみよう！というコンテストです。

というわけで、Coq でやってみて、力尽きました。難しいですね！コードだけ貼り付けておきます（提出はしてない）。

Problem 1

とある bool のソートアルゴリズム。

  • Coq で書けたので停止性は示されているはず
  • 配列は範囲内であることが証明されている整数でしかアクセスできない依存型なのでアクセスも安全なはず
  • 返値が sorted であることも証明付きの依存型なので大丈夫なはず
  • 元のpermutationであることは示せてない
Require Import ZArith Omega Zwf.
Require Import List Bool.
Require Import Program Relations Wellfounded.
Open Scope Z_scope.

(**
 * Definition of arrays of size [n] with element type [t].
 * They are indexed by 0 <= i < n and returns t.
 *)

Definition index (n: Z) := {i | 0<=i /\ i<n}.
Definition array (n: {n|n>=0}) (t: Type) :=
  forall (i: index (`n)), t.
Axiom proof_irrelevance :
  forall n t (a:array n t) i j, `i = `j -> a i = a j.

(**
 * Definition of swap.
 *)

Program Definition swap {n} {t} (a: array n t) (i j: index n) :=
  fun (k: index n) => if Z_eq_dec k i then a j
                 else if Z_eq_dec k j then a i
                                      else a k.

(**
 * Definition of sortedness
 *)

Program Definition sorted {n} (a: array n bool) :=
  forall i j, a i=false /\ a j=true -> i<j.

(**
 * The main loop.
 *
 * The algorithm in the problem statement is implemented.
 * Four invariants are hand-annotated and proven.
 *)

Local Obligation Tactic :=
 (program_simpl; unfold Zwf; try omega).

Program Fixpoint loop {n} (a: array n bool) (i j: Z)
  (* Loop invariants. *)
  (inv1: 0<=i /\ i<=n)
  (inv2: j<n)
  (inv3: forall (k: index n), k<i -> a k=false)
  (inv4: forall (k: index n), k>j -> a k=true)
  (* Termination measure: j-i is decreasing. *)
  {measure (j - i) (Zwf 0)}
  (* Return type assures sortedness *)
  : {a: array n bool | sorted a}
:=
  if Z_le_dec i j then
    if bool_dec (a i) false then
      loop a (i+1) j _ _ _ _                (*  4: inv3 *)
    else if bool_dec (a j) true then
      loop a i (j-1) _ _ _ _                (* 11: inv4 *)
    else
      loop (swap a i j) (i+1) (j-1) _ _ _ _ (*17,18: inv3,4*)
  else
     a.                                     (* 20: sorted *)

(* Discharging proof obligations. *)

Obligation 4.
  assert (X: `k=i \/ `k<i) by omega; destruct X;
    [rewrite <-H0|]; eauto using proof_irrelevance.
Qed.

Obligation 11.
  assert (X: `k=j \/ `k>j) by omega; destruct X;
    [rewrite <-H1|]; eauto using proof_irrelevance.
Qed.

Obligation 17.
  unfold swap.
  destruct Z_eq_dec. (* k=i *)
    rewrite <-(not_true_is_false _ H1).
    eauto using proof_irrelevance.
  simpl in n0.
  destruct Z_eq_dec. (* k=j *)
    assert (`k <> j) by omega.
    contradiction.
  (* other *)
    apply inv3; omega.
Qed.

Obligation 18.
  unfold swap.
  destruct Z_eq_dec. (* k=i *)
    simpl in e.
    rewrite <-(not_false_is_true _ H0).
    assert (i = j) by omega.
    eauto using proof_irrelevance.
  destruct Z_eq_dec. (* k=j *)
    rewrite <-(not_false_is_true _ H0).
    eauto using proof_irrelevance.
  (* other *)
    simpl in n1.
    apply inv4; omega.
Qed.

Obligation 20.
  unfold sorted; intros i0 j0 [Hi Hj].
  assert (~(`i0 >= i) /\ ~(i > `j0)).
  split.
    intro.
      assert (`i0 > j) by omega.
      rewrite (inv4 i0 H4) in Hi.
      auto using diff_true_false.
    intro.
      assert (`j0 < i) by omega.
      rewrite (inv3 j0 H4) in Hj.
      auto using diff_true_false.
  omega.
Qed.

(* Entry point *)
Program Fixpoint two_way_sort {n} (a: array n bool)
  : {a: array n bool | sorted a}
:=
  loop a 0 (n-1) _ _ _ _.

Obligation 3.
  destruct k; simpl in H; apply False_ind; omega.
Qed.
Obligation 4.
  destruct k; simpl in H; apply False_ind; omega.
Qed.

Problem 4

リストから、規則に従ってツリーを作る。

  • Coq で書けたので停止性は示されているはず
  • 健全性や完全性は示せてない
Require Import Arith Omega.
Require Import List.
Require Import Program Relations Wellfounded.
Local Obligation Tactic :=
  (program_simpl; simpl in *; try omega).

(**
 * Definition of trees and lists
 *)

Inductive tree :=
 | Leaf : tree
 | Node : tree -> tree -> tree.

Definition list := List.list nat.

(**
 * The implementation.
 *
 * Immutable list is used. So, the build_rec function returns
 * the list left after the procedure as well as the tree.
 * Also, failure is reprensented by the option type.
 *)

Program Fixpoint build_rec (d: nat) (s: list)
  (* Termination measure: lexicographic order on (|s|, h-d) *)
    {measure (match s with nil      => existT _ 0 0
                         | cons h _ => existT _ (length s) (h - d) end)
             (lexprod nat _ lt (fun _ => lt))}         (* 5 *)
  (* Return type with a post condition on length decreasing *)
    : option (tree * {t: list | length t < length s})
:=
  (* The algorithm written in the problem statement. *)
  match s with
  | nil      => None
  | cons h t => if lt_dec h d     then None
           else if eq_nat_dec h d then Some (Leaf, t)  (* 1 *)
           else match build_rec (d+1) s with           (* 2 *)
                | None        => None
                | Some (l, s) =>
                  match build_rec (d+1) s with         (* 3 *)
                  | None        => None
                  | Some (r, s) => Some (Node l r, s)  (* 4 *)
                  end
                end
  end.
  (** Discharge proof obligations.
   *    1,4 : Returned list gets shorter (auto).
   *    2,3 : Argument is decreasing.
   *    5   : Wellfoundedness of the termination measure.
   *)
  Obligation 2.
    right; omega. (* h-d is decreasing. *)
  Qed.
  Obligation 3.
    destruct s0; left; simpl in *; omega. (* |s| decreases. *)
  Qed.
  Obligation 5.
    auto using measure_wf, wf_lexprod, lt_wf.
  Defined.

Definition build (s: list) : option tree :=
  match build_rec 0 s with
  | Some (t, exist nil _) => Some t
  | _                     => None
  end.

(**
 * Test cases (run in OCaml).
 *)

Definition test1_in  := [1;3;3;2].
Definition test1_out := Some (Node Leaf (Node (Node Leaf Leaf) Leaf)).

Definition test2_in  := [1;3;2;2].
Definition test2_out := @None tree.

Extraction "extracted.ml" build test1_in test1_out test2_in test2_out.

test.ml

#use "extracted.ml"

let _ = 
  assert (build test1_in = test1_out);
  assert (build test2_in = test2_out);
  print_endline "[TEST PASSED]"

Coqの入門記事を書く会 (4)

Coq

今回は、入門記事書きはちょっと休憩して、Coqの解説記事などを集める会です。

英語

言語そのものを浅く/深く眺めていく、という方向のテキスト３つ：


講義の素材として作られたチュートリアル達。より具体的な題材での演習付きなので面白いかも：


Coqの使い方はわかる、という人が、その先「Coqの良い上手い使い方を学ぶ」ための本。

日本語

自然数とリスト: まとめ (3.7)

Coq

駆け足でいろいろ紹介しました。

  • SearchAbout でライブラリを検索
  • 自然数やリストはInductiveなデータ
  • = に関する証明 reflexivity, symmetry, transitivity, discriminate
  • = を使った書き換え rewrite, replace
  • 計算をすすめる simpl, cbv, ...
  • 自動証明 omega, ring, field, ring_simplify, field_simplify
  • 帰納法 induction
    • intro しすぎにご用心。generalize
    • 整礎帰納法
  • exists

当初の予定では3回くらいにわけるつもりだったんですが、めんどくさくなったので一気に書いてしまうことにしました。駆け足すぎてよくわからなくなってしまってると思いますが、他の入門記事やチュートリアルなどと併用してください（いい加減になってきた…）。ではでは。

追伸

そういえば、このシリーズでは intros や destruct では自分で仮定に名前をつけることはせずに、Coqの自動生成にまかせちゃっているんですが、これって、コーディングスタイルとしては良くないのかもしれません。ということにさっき気づきました。H0 やら H1 やらではよく分からないですよね。本当は、ちゃんと名前をつけて intros 等した方がいいと思います！

自然数とリスト: exists (3.6)

Coq

ここまで forall, ->, and, or, not のCoqでの使い方を見ました。Wikipediaの一階述語論理のページなどを見てみると、もう一種類、この手の論理結合子があります。∃（存在する）。Coq では、exists と書きます。

Theorem even_or_odd:
  forall (n:nat), exists m, (n=2*m \/ n=2*m+1).
Proof.
  induction n.

「どんな自然数 n に対しても、自然数 m が存在して、(n=2*m \/ n=2*m+1) を満たす」。こういう「これこれこういう値が存在します」という主張の定理を書くために使います。

証明してみましょう。帰納法でやります。induction n。

0の場合とそれ以外の場合にゴールが分かれますが、まずは0の方から。nを0に置き換えた

-------------------------------
exists m:nat, 0=2*m \/ 0=2*m+1

これを証明しないといけません。どうしましょう。existの正体を見てみると Coq.Init.Logic.ex:

(* Remark: exists x, Q denotes ex (fun x => Q) ... *)
Inductive ex (A:Type) (P:A -> Prop) : Prop :=
  ex_intro : forall x:A, P x -> ex (A:=A) P.

これも Inductive な命題です。exists x, P を証明するための公理は「"具体的な値 x" と "P x の証明" があれば、ex P が証明できる」という ex_intro。要するに、「Pであるようなxが存在する」を証明するには、具体的にそのxの値を人間が思いついて、Coqさんに教えてあげないといけません。

今回の場合、0=2*m \/ 0=2*m+1 を満たすような m は… m=0 とすれば成り立ってますね。これを Coq に教える tactic は、命題の記述と同じなのでちょっとややこしいですが、exists です。

 exists 0.

これで、ゴールが 0=2*0 \/ 0=2*0+1 に変わります。あとは簡単。

 left.
 simpl.
 reflexivity.

exists 0. の代わりに、Inductiveなゴールの証明の仕方の基本通り、"apply コンストラクタ" で書くこともできます: apply (ex_intro _ 0). が、やや面倒なのでexists tacticを使うのがよいと思います。

帰納法のもう一つのケースはこちら。

n : nat
IHn : exists m : nat, n = 2 * m \/ n = 2 * m + 1
--------------------------------------------------
exists m : nat, S n = 2 * m \/ S n = 2 * m + 1

今度は仮定の方にもexistsが出てきますが、Inductiveなものが仮定にでききたらdestruct IHn. こう変わります。

n : nat
x : nat
H : n = 2 * x \/ n = 2 * x + 1
--------------------------------------------------
exists m : nat, S n = 2 * m \/ S n = 2 * m + 1

「ほにゃららな自然数 m が存在する」という仮定を、「自然数 x がある」「x はほにゃららを満たす」と分解してくれます。

仮定 H がまだ \/ の形なのでさらに分解 destruct H. すると、ゴールが２つに分裂して、１つめはこう。

H : n = 2 * x
--------------------------------------------------
exists m : nat, S n = 2 * m \/ S n = 2 * m + 1

さて、n=2*x という仮定の下で、m をどうすれば S n = 2 * m \/ S n = 2 * m + 1 が成り立つようにできるか。ここはうんうん唸って考えましょう。m=x とすれば、∨の右側が成り立ちます。

 exists x.
 right.
 omega.

もう一つのゴールは

H : n = 2 * x + 1
--------------------------------------------------
exists m : nat, S n = 2 * m \/ S n = 2 * m + 1

こうですが、今度は、m=x+1 とすると、左が成り立ちます。

 exists (x+1).
 left.
 omega.
Qed.

まとめ。

exists e.
exists x, P という形のゴールを示すときに、x=e とすれば示せますよ！と具体的な値をCoqさんに教える方向で証明する。
仮定にexistsが出てきた場合は、destructが使えます。


たぶん、Coqを使った証明で一番直接的に難しいのは、exists の証明です。これを証明するには、具体的にどの値を当てはめれば成り立つのか、完全に人間が考えてあげないといけません。今回だと、こっちの場合はm=xで行ける、こっちだとm=x+1…と言った具合に。数学の教科書などでは「十分大きな x を取れば P x が成り立つから exists x, P x」のような言い方をしたりしますが、こういう時でも、十分大きい x とは具体的にいくつなのか、100なのか65536なのか無量大数なのか、中身が実際に証明できる大きさを明確に書く必要があります。

などは、直感的には対して難しくない定理なはずなんですが、この難しさのせいで結構な難問になってるように思います。

適度な練習問題としては、さきほども紹介しましたが、

などなど。

Setバージョン

前回、A∨B には、よく似た意味の {A}+{B} というものがある、という紹介をしました。違いは、前者が Prop で後者が Set なことですが、証明の仕方はだいたい同じです。exists x, P にも同じ関係の {x | P} という Set バージョンがあります（Coq.Init.Specif.sig）。

などに登場します。この問題の

Definition tails {A:Set} (ys: list A) : {xss | all_suffixes xss ys}.

は、だいたい

Theorem tails:
 forall (A:Set) (ys: list A), exists xss, all_suffixes xss ys.

と同じ意味です。証明も全く同じく、exists と destruct でできます。違いは、{_}+{_} の場合と同じく、「ゴールがSetのときはPropをdestructできない」という制約のみ。この制約の意味するところについては、次回ご紹介したいと思います。

自然数とリスト: 帰納法の色々 (3.5)

Coq

Coqでの帰納法の仕組みについて、ちょっとだけ。CoqIDE に

Inductive nat :=
 | O : nat
 | S : nat -> nat.

と打ち込んで nat を再定義してみてください。

nat is defined
nat_rect is defined
nat_ind is defined
nat_rec is defined

こう右下に表示されると思います。実は、nat を定義すると同時に、裏でひっそりと3つの公理がCoqによって自動で定義されているのです。これが帰納法の正体です。

Print nat_ind.

こんな命題です。

nat_ind =
fun P : nat -> Prop => nat_rect P
     : forall P : nat -> Prop,
       P O -> (forall n : nat, P n -> P (S n)) -> forall n : nat, P n
  • 自然数に関するどんな命題 P : nat -> Prop も、
    • 0 で成り立つ P O 証明
    • n で成り立 P n てば、S n でも成り立つ P (S n) という証明
    • の二つがあるなら forall n : nat, P n すべての n で成り立つ

と書いてあります。まさに帰納法です。induction n. という tactic は、基本的には、実は apply nat_ind. しているだけだったりします（実際はゴールに n が複数あるときの扱いなど、induction n の方が便利になるように工夫が入っていますけど）。

Require Import List.
Print list_ind.

すると list の帰納法も見られます。

False_ind

and や or など再帰的じゃないInductiveにも、一応機械的に帰納法の公理が定義されているのですが、あんまり使い道はありません。唯一使えるのが False のために自動定義される False_ind で

Print False_ind.

False_ind = 略 : forall P : Prop, False -> P

どんな命題 P も、「False が成り立っているなどというあり得ない事態であれば、成り立つ」。これを使うと apply False_ind. で、どんなゴールも False に変えられます。仮定がそもそもおかしいときに「仮定がそもそもおかしいぞ」とCoqさんに伝えるのに使います。apply False_ind してから普通にFalseを証明してしまえばよし。さきほど紹介した condtraction H. があれば普通は用が足りますが、仮定にそのまま１個でバシッと矛盾しているものを作るのが難しいときには、「Falseを証明する」方が楽だったりします。

カリーハワード

さて、カリーハワード対応の時間です。「帰納法」とは、プログラミングで言うと、何にあたるのでしょうか。

list_ind =
fun (A : Type) (P : list A -> Prop) => list_rect P
     : forall (A : Type) (P : list A -> Prop),
       P nil ->
       (forall (a : A) (l : list A), P l -> P (a :: l)) ->
       forall l : list A, P l

答えは、foldr です。Haskell には"依存型"がないので、"P nil" や "P l" の部分が全部同じ型 b になって簡単化してますが、やっていることは同じで

  • nil の場合の結果
  • cons x xs の場合、x と "xs を foldr して結果" から計算結果を求めて返す関数

の二つから、任意のリストを受け取ってリスト全体を計算して返す関数を作るのがfoldrであります。

整礎帰納法

「数学的帰納法」って、こうじゃなかったけ？と記憶されている方もいらっしゃるかもしれません。

  • nより小さい全ての数で成り立つなら、nでも成り立つ

が言えれば、「全てのnで成り立つ」と言える。

これは 整礎帰納法 と呼ばれる証明方法で、普通の帰納法よりさらに強力なテクニックです。Sqrt 2 @ Anarchy Proof などではたぶんこれが使いたくなると思います。

Coqでは自然数に関する整礎帰納法はCoq.Arith.Wf_natというモジュールで定義されていて、

Requirt Import Wf_nat.
Print lt_wf_ind.

lt_wf_ind =
 中略
     : forall (n : nat) (P : nat -> Prop),
       (forall n0 : nat,
        (forall m : nat, m < n0 -> P m) -> P n0) ->
       P n

こうです。読んで字のごとしです。使うには直接

 apply lt_wf_ind.

するか、induction 〜 using という tactic を使います。帰納法っぽいtacticを使いやすくapplyしてくれるものです。

 induction n using lt_wf_ind.

ある条件を満たす順序関係があれば、自然数以外でも整礎帰納法は使えます。詳しくは Coq.Init.Wf。

introしすぎにご用心

さっきの例題を、ちょっとだけ形をいじって

Require Import Arith Omega.

Fixpoint sum (n: nat) :=
  match n with
  | O => 0
  | S m => n + sum m
  end.

Theorem Sum_of_nat:
 forall (n m: nat),
   m = 2 * sum n -> m = n*(n+1).
Proof.

こうしたものを考えます。

 intros.
 induction n.

こうすると、n=0 の場合まではなんとかなる（rewrite H. simpl. reflexivity.）のですが、S n の場合が

H : m = 2 * sum (S n)
IHn : m = 2 * sum n -> m = n * (n + 1)
---------------------------------------
m = S n * (S n + 1)

帰納法の仮定 IHn が、何かちょっと困った形になってしまいます。これは、全部 intros してから induction すると、「intros で仮定に押し上げて m を固定してしまった状態で帰納法を回す」ことになってしまうせい。正しくは

 forall (m:nat), m=2*sum n -> m = n*(n+1)

というように、m がforallされた命題が、全てのnで成り立つことを証明しないとうまくいきません。

ということで、intros ではなく、intro で n だけ剥がしてから induction しましょう。（実は induction tactic は便利に作られていて、なにもintroせずにinduction nと書いたら自動で n まででintroを止めてinducitonを始めてくれるので、それでも可です。）

Proof.
 intro n.
 induction n.

 (以下は練習問題)

「forall や -> を見たらとりあえず intros 」という方針をこれまで推奨してきましたが、induction を使う前に限っては、必要最小限の intro で 止めておく方がうまくいくことが多いようです。

実は、もっといじわるなバージョンも考えられます。

Theorem Sum_of_nat:
 forall (m n: nat),
   m = 2 * sum n -> m = n*(n+1).
Proof.

今度は、m の方が n より先にあるため、n だけを intro しようとしても無理で、intros m n. のように、必ず m も仮定に引っ張り上げてしまいます。こういう時には、仕方なく intros してから、"generalize" という tactic で、仮定を forall に戻します。

 intros m n.
 generalize m.
 induction n.

あとはさっきと同様。

自然数とリスト: 帰納法 (3.4)

Coq

別の問題を証明してみましょう。Anarchy Proof から Sum of natural numbers をお借りします。ring を使わないでやってみよう、という問題ですが、気にせずringを使って解いちゃいますので、ネタバレにはなっていないはず…。

Require Import Arith Omega.

Fixpoint sum (n: nat) :=
  match n with
  | O => 0
  | S m => n + sum m
  end.

Theorem Sum_of_nat:
 forall (n: nat),  2 * sum n = n * (n + 1).
Proof.
 intros.
 destruct n.

まずは、ここまでで解説したtacticを使って挑戦してみます。実はそれではうまくいかないのですが、しばらくおつきあい下さい。

1つめのゴール、n=0の場合の 2*sum 0=0*(0+1)は簡単です。

 simpl.
 reflexivity.

両辺計算すると 0 になるので、0=0 は reflexivity で。simpl は計算できるところは計算して下さい、というtacticです。計算させるtacticはsimplの他にhnf、compute、cbv、lazy、vm_computeなどがありますが詳細はリファレンスなどをご覧下さい。そこそこ適当に計算するのがsimpl、本気でできる限り計算するのがcbv、くらいの感覚で。ringとfieldの性質を使って式を整理する、ring_simplify、field_simplify というのもあります。

もう一つのゴールが問題です。simpl すると…まだごちゃごちゃしているので、さらに ring_simplify すると

 simpl.
 ring_simplify.

n:nat
-----------------------------------
2*n + 2*sum n + 2  = n*n + 3*n + 2

こうなります。これは、もし 2*sum n = n*n + n が成り立てば、ゴールの中の 2*sum n を rewrite すれば左辺と右辺が同じになるのですが、それって、今証明しようとしている式ほとんどそのまんまです。堂々巡り。

こういう時に使うのが、数学的帰納法です。Coqでは、Inductiveな物をdestructする代わりに、inductionというtacticで分解します。

Theorem Sum_of_nat:
 forall (n: nat),  2 * sum n = n * (n + 1).
Proof.
 intros.
 induction n. (* destruct n の代わりに！ *)

 simpl.
 reflexivity.

 simpl.
 ring_simplify.

さっきと同じ証明をすると、今度は…

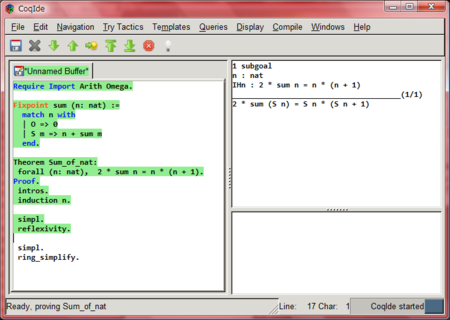
仮定に IHn : 2 * sum n = n * (n+1) という便利な等式が入っています！

 rewrite IHn.
 ring.
Qed.

証明完了。

数学的帰納法についておさらいしておくと、自然数の場合、

  • n=0 で命題（たとえば 2 * sum 0 = 0 * (0 + 1)）が成り立つ
  • nで成り立つなら、S n でも（2 * sum (S n) = S n * (S n + 1)）成り立つ

この二つが証明できたなら、その命題はすべての自然数 n で成り立つ！という証明方法です。一方で destruct での証明は

  • n=0 で命題（たとえば 0<>0 -> 0<0+0）が成り立つ
  • S n でも（0<>S n -> S n < S n + S n）成り立つ

の二つが証明できたら、すべての自然数 n で成り立つ、という証明です。帰納法の方が、"nで成り立つなら" という仮定を使える分、強力なわけですね。

帰納法の考え方は、自然数だけではなく、再帰的に定義された（つまり、S : nat -> nat のようにコンストラクタが作りたいものと同じ型を引数にとる）Inductive すべてに一般化できます。リストの場合

  • xs=nil で成り立つ
  • xs で成り立つなら、cons x xs でも成り立つ

が言えれば、その命題は全てのリストで成り立つことが証明できます。

ここまでの総まとめの練習問題としては

などいかかでしょうか…と思ったら、まだ exists の説明してないですね。これはあとで。(3.6)でやります。

自然数とリスト: 自動証明 (3.3)

Coq

Coqさんは非常に賢いので、実は、今回くらいの証明は自動でやってくれます。

Proof.
 intros.
 omega.
Qed.

omega はプレスバーガー算術という美味しそうな名前の理論の簡易全自動ソルバーで、整数に関する等式や不等式のかなりの部分を自動的に証明してくれます。

omega
整数/自然数の、足し算引き算や定数倍に関する、等式や不等式を自動証明。変数と変数の掛け算があると使えない。
ring
足し算引き算掛け算に関する等式を、単に式を整理することで自動証明。不等式は使えない。
field
足し算引き算掛け算割り算に関する等式を、単に式を整理することで自動証明。不等式は使えない。
fourier
実数に関する線形不等式の自動証明
これらがないと、数式の証明はひたすらSearchAboutとrewriteを繰り返す退屈な作業になってしまうことが多いので、覚えておかないと大変です。数式の証明で困ったらomega! この入門記事シリーズでも、今後はomega/ring/fieldで証明できるところは使っていきます。