ひとり勉強会

ひとり楽しく勉強会

andとorとnot: デストラクト (2.4)

Coq

「コンストラクタがあるならデストラクタはないんですか」

あるのです。これを語らなくては話が終わりません。コンストラクタの逆の話なので、例題も逆にしましょう。ド・モルガンの法則は逆向きにも成り立ちます。

Lemma De_Morgan2:
 forall A B: Prop, (~A /\ ~B) -> ~(A \/ B).
Proof.
 unfold not.
 intros.

とりあえず unfold と intros してみるのは良いとして…

次、どうしましょう。仮定にあるのは

  • H: (A->False)∧(B->False)
  • H0: A∨B

だけで、-> がないので、もう apply もできません。困った。

逆に考えるんだ。

  • 「∧を証明できるのは公理 conj: hoge→fuga→hoge∧fuga しか存在しない」
  • 既に仮定 H に「(A->False)∧(B->False)」がある
  • これは conj に「A->False」と「B->False」を渡して作ったとしか考えられない

なので、「(A->False)∧(B->False)」を仮定しても良いなら、同時に、「A->False」と「B->False」も既に成り立っていると仮定して良いでしょう！

と Coq さんに伝えるのが、destruct という tactic です。

 destruct H.

仮定から∧が消えて

  • H: A->False
  • H1: B->False
  • H0: A∨B

こう分解されます。「A∧Bを仮定してCが証明できる」ことを示すには、「AとBを仮定してCが証明できる」ことを示せば十分、と仮定を分解するのがdestructです。

もう一個、仮定に、分解できそうな子がいますね。

  • 「∨を証明できるのはor_introlかor_introrのどちらかしかない」
  • 既に仮定に H0: A∨B がある。これは
    • 「or_introl に A を渡して作った」か
    • 「or_intror に B を渡して作った」のどっちかしかあり得ない。

どっちかわからないけど、両方の場合を考えてどっちもゴールが証明できたらOKじゃない？とCoqさんにお願い。

 destruct H0.


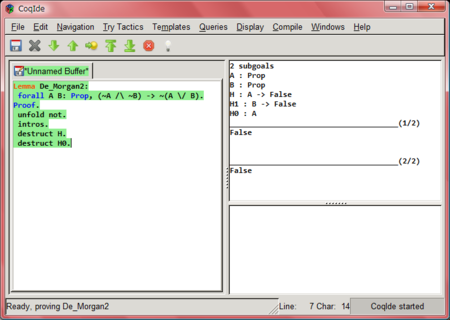
「A∨Bを仮定してCが証明できる」ことを示すには、「Aを仮定してCが証明できる」と「Bを仮定してCが証明できる」の二つのゴールを証明すればよいのです。というわけでゴールが２つにわかれます。

ここまで来れば簡単ですね。

 exact (H H0).
 exact (H1 H0).
Qed.

まとめると…

Inductiveでユーザー定義した命題の公理（conj や or_introl や or_intror）は、「それを使うとユーザー定義命題を証明できる」という意味と、「それ以外の方法では決して証明できない」という、２つの意味があります。前者の性質を使うのがコンストラクタによる証明で、後者を使うのがdestruct tacticによる証明です。

destruct H.
仮定Hの型TがInductiveで、そのコンストラクタが A->B->T、C->D->T、E->F->T、… だったら、「Hを仮定してゴールを示す」という状態を「AとBを仮定してゴールを示す」「CとDを仮定してゴールを示す」「EとFを仮定してゴールを示す」…に分解する
destruct H as [HA HB].
destruct H as [HA|HB].
destruct H as [HA [HB HC] ].
説明してませんでしたが、destructした時に新しく増える命題にはasで名前をつけることができます。andのようにゴールが分岐せず仮定が増える部分には[HA HB]と並べ、orのようにゴールが増える部分には[HA|HB]と並べます。ネストさせるとA∧B∧Cみたいなのを一気にdestructしたりできます。詳しくはリファレンスをどうぞ。
decompose [and or] H.
実はわたしは使ったこともちゃんと調べたこともないのですけど、賢く全部destructしつくしてくれる感じのtactic？
elim H
case H
destruct よりももっとプリミティブな操作です。destructすると「元々あった仮定を消して新しく分解後の仮定を追加」しますが、elim を使うと「元々の仮定は消さない。分解後の結果は過程に追加するのではなく、ゴールに->で追加」します。さらに、「分解した仮定Hが他の仮定の中に使われていた場合にそのHも書き換える」がdestructで書き換えないのがelim。まあなんだかややこしいのですが、要は、「destructはちょっとやり過ぎで困る」と思ったらelimに変えて試してみるといいかも…。
まあ、ややこしいことは気にせず仮定にInductiveなものがあったらとりあえずdestructしてみるという証明戦略は結構うまくいく気がします。

ややこしいことは気にせずといえば、カリーハワード対応脳の人には、destructのもっとずっとわかりやすい説明があります。要するにこれは、

Print De_Morgan2.

De_Morgan2 =
fun (A B : Prop) (H : (A -> False) /\ (B -> False)) (H0 : A \/ B) =>
match H with
| conj H1 H2 =>
    match H0 with
    | or_introl H3 => H1 H3
    | or_intror H3 => H2 H3
    end
end

パターンマッチなのです。