ひとり勉強会

ひとり楽しく勉強会

自然数とリスト: rewriteなど (3.2)

Coq

x=0の場合は終わったので、残ったゴールはこれです。

-------------------------
S x < S x + S x

これを証明するには…なにか、このくらいはさっきImportしたArith標準ライブラリで証明されていないでしょうか。CoqIDEでは

SearchAbout (_ < _ + _).

と打ち込むか、F2キーを押して (_ < _ + _) を検索すると…

「(_ < _ + _) という形のゴールに apply できそうなライブラリ定理の一覧」が表示できます。便利です。

表示された一覧の中に、わたしが見た限りでは直接使えそうなものはなかったのですが、近い物がありました。

plus_lt_compat_l : forall n m p: nat, n<m -> p+n < p+m

これ。p+n < p+m というのは S x < S x + S x の形にはなっていませんが、これを使えば "S x + 0 < S x + S x" なら証明できそう。"S x" と "S x + 0" は等しいので、これが示せれば十分ですよね。

十分ではありません。まず「"S x" と "S x + 0" は等しい」から証明してあげないとCoqさんは納得してくれません。納得させます。

 assert (S x = S x + 0).

初回にやった assert (X:=t) というtacticは、tという証明を書いて、その型の命題を仮定に追加するものでした。今回の assert (命題) は、「(命題)が成り立つので仮定に足してくれ！証明は今からやる！」とCoqさんに伝えるものです。

assertすると、メインの証明はいったん脇に置いておいて、assertされた命題の証明モードに入ります。ゼロを足しても値は等しい、というのは流石に標準の定理にあって、SearchAbout (_ = _ + 0). するとすぐ見つかりますので、それをapplyすれば証明完了。

 apply plus_n_O.

証明が１行で書ける場合は

 assert (S x = S x + 0) by apply plus_n_O.

と assert 〜 by でまとめて書いちゃうこともできます。

assert P.
メインの証明のことは一端忘れて、P を証明するモードに入る。終わったら、メインの証明のなかで P を仮定として使えるようになる
assert P by tac.
Pの証明が1行で書ける場合。Pを仮定に追加。
cut P.
assertと順番が逆になったもの。ゴールが "P->今のゴール" に変わる。ただし、それが終わった後にPの証明をしないといけない。

assertで脇道にそれましたが、無事に仮定が増えて、こうなっているはずです。

H0: S x = S x + 0
-------------------------
S x < S x + S x

ここで、「"S x" は "S x + 0" に等しいとわかっているんだから、ゴールにある "S x" は "S x + 0" に書き換えてよ！」とCoqさんに伝えるtacticが、rewrite。

 rewrite H0 at 1.

"at 1" は"１個目の" S xを書き換えてね、の意味です。これを指定しないとゴールが(S x + 0) < (S x + 0) + (S x + 0) に全部変わってしまって困ります。"at 1" なら

-------------------------
S x + 0 < S x + S x

狙い通りにこの形になってくれるので、使いたかったライブラリ定理 plus_lt_compat_l : forall n m p: nat, n p+n < p+m が使えます。

 apply plus_lt_compat_l.

ゴールが 0 < S x に変わりますが、SearchAbout (0 < S _). で、ピッタリの定理が見つかります。

 apply lt_O_Sn.
Qed.

まとめ。

rewrite H (at p1 p2 ....)
e1 = e2 の形の仮定 H があるときに、ゴールの中のe1をe2に書き換え。at ... があるときは、指定した番号のe1のみを書き換え。
rewrite <-H.
e1 = e2 の仮定 H を使って、逆向きに、e2をe1に書き換え
rewrite (<-)H in H1.
ゴールじゃなくて別の仮定H1の中を書き換え
今回は使いませんでしたが、assert + rewrite は非常によく使うので、replace、という複合tacticも用意されています。
replace e1 with e2.
まず、e1=e2を証明するモードに入る。証明できたらゴールの中のe1をe2に書き換え。
replace e1 with e2 by tac.
tac 1行でe1=e2を証明。さらに、ゴールの中のe1をe2に書き換え。
残念ながら replace には "at" 指定がないので、今回は使いませんでした。atが要らないときはreplaceがおすすめです。

自然数とリスト: Inductive (3.1)

Coq

前回、andやorなどの命題が"Inductive"で作られてることをご紹介しました。Coqでは、命題だけでなく、自然数やリストなどなど、普通のデータ型も、Inductiveで定義します。

例えば自然数は Coq.Init.Datatypes.nat

Inductive nat : Set :=
  | O : nat
  | S : nat -> nat.

こう。O (大文字のオーです) は、0 (ゼロです) を表します。S n は「n の一つ後ろの数」を表します。S (S (S O))) は 3。（ただし、実際に大量に S を並べるのは大変なので、Coq のコードでは 100 や 200 と普通に書けば勝手に処理系がS S ... (S O)と解釈してくれます。実体は S S S ... なので、10000 とか大きい定数を書くと結構大変なことになりますが…）

リストは Coq.Lists.List.list:

Variable A : Type.

Inductive list : Type :=
  | nil : list
  | cons : A -> list -> list.

Infix "::" := cons (at level 60, right associativity) : list_scope.

nil で空リストを作るか、cons で、リストに要素を一個足すか、どちらかの方法でリストは作れるし、その方法で作れるものだけがリストです。

さてさて、では早速、この辺りが登場する証明をやってみましょう。まずは簡単なものから。「x が 0 じゃない自然数なら、x+x は x より大きい」。

Require Import Arith Omega.

Lemma double_is_big:
 forall (x:nat), x <> 0 -> x < x+x.
Proof.
 intros.

1行目の Require Import ですが、Arith と Omega という二つの「ライブラリ」をこれから使います、とCoqさんに伝えています。どちらもCoqの標準ライブラリで、Arithには自然数に関する基本的な定理が大量に証明されて入っています。自然数の証明をする場合、とりあえずRequire Importしておくと良いと思います。Omegaについては後で。

さて、続きは…色々なやり方があります。ここで紹介するのはあくまで一例ですので、皆様もっと綺麗な証明を探してみて下さい。

仮定の所に x: nat とあります。仮定にInductiveなものがあわられたら、destructして分解してみる。これはandやorでなくても、命題じゃない、自然数のようなデータ型でも使えます。

 destruct x.

natには二つコンストラクタがあったので、ゴールが2つに分かれます。Oで作ったnatの場合（つまりx=0の場合）と、Sで作ったnatの場合です、0の方は、こんな風になります。

H: 0 <> 0
--------------
0 < 0 + 0

0 < 0+0 って成り立ってないので証明できなさそうな気がしますが、これは、仮定の方がおかしいのです。"H: 0<>0 ならば"…といわれても、そんなことはあり得ません！ということを証明したら、全体を証明したことになります。

そういえば説明し忘れましたが、x <> y は "~(x=y)" のシンタックスシュガーです。x=yではない。

 unfold not in H.

すると "H: 0=0 -> False" に変わることで確認できます（注：確認だけなので、これはやってもやらなくても以下の証明には変化ありません）。unfold 〜 in で、ゴールの中だけではなく仮定の中もunfoldできます。

「仮定に成り立たない命題が入ってるぞ」ということをCoqに伝えるのは、contradictionというtacticです。

 contradiction H.

contradiction H.
仮定 H: A1->A2->...->An->False があったら、ゴールを、A1とA2と...とAnのn個のゴールに変える
仮定などに "H: False" があったらいきなりこれでゴールが0個になるので証明完了します。（練習問題： False @ AnarchyProof）

今回の例は "0=0 -> False" なんて仮定は成り立ちませんよ！とcontradictionしたので、証明すべき命題は 0=0 です。

 reflexivity.

そりゃ当たり前に = ですよね、とCoqさんに伝えます。イコールに関するtacticは以下の4種類です。

reflexivity.
e = e の形のゴールを証明
symmetry.
e1 = e2 というゴールを e2 = e1 に変える
symmetry in H.
e1 = e2 という仮定Hを e2 = e1 に変える
transitivity e3.
e1 = e2 というゴールを e1 = e3 と e3 = e2 の２つに変える
discriminate H
S x = O や、nil = cons x y のような、「違うコンストラクタで作ったデータが等しいと主張するありえない仮定」H があったら、それは無理ですよ、とCoqさんに伝えて証明完了

Coqの入門記事を書く会 (3)

Coq

このペースだと、なかなかCoqの一番面白いところ（とわたしが思うところ）に行き着かないので、今回は全力ですっ飛ばして、必要な細かい話を全部片付けちゃおうと思います。次回が面白くなるはずです。今回は、主に、自然数やリストにまつわる証明の巻。

andとorとnot: 次回予告 (2.6)

Coq

もう今回の内容でInductiveの扱いは完璧…！

といいたいところなんですが、「再帰的なInductive」の証明テクニックの解説が実はまだ残っています。次は多分それについて書きたいなあと思っています。それかFalse周りの証明をさらにいろいろ。

andとorとnot以外のInductive (2.5)

Coq

何度か繰り返しているように、andやorやFalseは、Coqに組み込みの摩訶不思議な何かではなく、ユーザー定義できる命題です。andやorに使える証明方法は、他のInductive命題にもそのまま使えます。試しに他に何か自作してみましょう。

こんなの考えてみました。

Inductive major (A B C:Prop) : Prop :=
| ab : A->B->major A B C
| bc : B->C->major A B C
| ca : C->A->major A B C.

AとBとCのうち、2個以上が成り立つなら成り立つ、多数決命題 major A B C を定義しました。例えば、こんな定理が成り立ちます。

Theorem majmaj:
 forall A B C: Prop,
   major A B C -> ~major (~A) (~B) (~C).
Proof.

とりあえず unfold not. して、intros. して…あとは仮定に major ばっかりになるので、Inductive な命題が仮定にあるときは…？ 練習問題です(^^)。


他に重要な例としては、Anarchy Proof の問題でも時々でてきます（Prime is decidable など）が、{A}+{B} というのがあります。これの定義はCoq.Init.Specif.sumbool:

Inductive sumbool (A B:Prop) : Set :=
  | left : A -> {A} + {B}
  | right : B -> {A} + {B} 
 where "{ A } + { B }" := (sumbool A B) : type_scope.

コンストラクタの名前が違うだけで、ほとんど A∨B と同じです。実際、∨を{}+{}に変えた

Lemma De_Morgan3:
 forall A B: Prop,
  ({A}+{B}->False) -> ((A->False) /\ (B->False)).

でも

Lemma De_Morgan4:
 forall A B: Prop,
  ((A->False) /\ (B->False)) -> ({A}+{B}->False).

でも、全く同じに、"constructor" と "destruct" を使って証明できます。試してみて下さい。練習問題です(^^)。こんな風に、見たことのない新しい命題が現れても、どれもandやorと同じく、constructorとdestructで証明にとりかかれます。簡単ですね。


※ {A}+{B} に関しては、A∨B と唯一違うところは、∨の方は:Propと宣言されてましたが、{}+}{}の方は:Setと宣言されているところです。PropとSetの違いはそのうち多分説明するような気がしますが、とりあえず証明を考える際に問題となる違いは１点だけ。

  • ゴールが Set のときは、Prop の destruct はできない

この制約のせいで、"forall A B:Prop, {A}+{B} -> A\/ B" は証明できますが、"forall A B:Prop, A\/ B -> {A}+{B}" はできません。この形になってしまったときは、destructを使わずになんとか迂回して証明することになります。

andとorとnot: デストラクト (2.4)

Coq

「コンストラクタがあるならデストラクタはないんですか」

あるのです。これを語らなくては話が終わりません。コンストラクタの逆の話なので、例題も逆にしましょう。ド・モルガンの法則は逆向きにも成り立ちます。

Lemma De_Morgan2:
 forall A B: Prop, (~A /\ ~B) -> ~(A \/ B).
Proof.
 unfold not.
 intros.

とりあえず unfold と intros してみるのは良いとして…

次、どうしましょう。仮定にあるのは

  • H: (A->False)∧(B->False)
  • H0: A∨B

だけで、-> がないので、もう apply もできません。困った。

逆に考えるんだ。

  • 「∧を証明できるのは公理 conj: hoge→fuga→hoge∧fuga しか存在しない」
  • 既に仮定 H に「(A->False)∧(B->False)」がある
  • これは conj に「A->False」と「B->False」を渡して作ったとしか考えられない

なので、「(A->False)∧(B->False)」を仮定しても良いなら、同時に、「A->False」と「B->False」も既に成り立っていると仮定して良いでしょう！

と Coq さんに伝えるのが、destruct という tactic です。

 destruct H.

仮定から∧が消えて

  • H: A->False
  • H1: B->False
  • H0: A∨B

こう分解されます。「A∧Bを仮定してCが証明できる」ことを示すには、「AとBを仮定してCが証明できる」ことを示せば十分、と仮定を分解するのがdestructです。

もう一個、仮定に、分解できそうな子がいますね。

  • 「∨を証明できるのはor_introlかor_introrのどちらかしかない」
  • 既に仮定に H0: A∨B がある。これは
    • 「or_introl に A を渡して作った」か
    • 「or_intror に B を渡して作った」のどっちかしかあり得ない。

どっちかわからないけど、両方の場合を考えてどっちもゴールが証明できたらOKじゃない？とCoqさんにお願い。

 destruct H0.


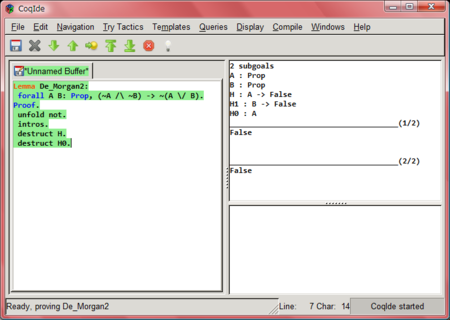
「A∨Bを仮定してCが証明できる」ことを示すには、「Aを仮定してCが証明できる」と「Bを仮定してCが証明できる」の二つのゴールを証明すればよいのです。というわけでゴールが２つにわかれます。

ここまで来れば簡単ですね。

 exact (H H0).
 exact (H1 H0).
Qed.

まとめると…

Inductiveでユーザー定義した命題の公理（conj や or_introl や or_intror）は、「それを使うとユーザー定義命題を証明できる」という意味と、「それ以外の方法では決して証明できない」という、２つの意味があります。前者の性質を使うのがコンストラクタによる証明で、後者を使うのがdestruct tacticによる証明です。

destruct H.
仮定Hの型TがInductiveで、そのコンストラクタが A->B->T、C->D->T、E->F->T、… だったら、「Hを仮定してゴールを示す」という状態を「AとBを仮定してゴールを示す」「CとDを仮定してゴールを示す」「EとFを仮定してゴールを示す」…に分解する
destruct H as [HA HB].
destruct H as [HA|HB].
destruct H as [HA [HB HC] ].
説明してませんでしたが、destructした時に新しく増える命題にはasで名前をつけることができます。andのようにゴールが分岐せず仮定が増える部分には[HA HB]と並べ、orのようにゴールが増える部分には[HA|HB]と並べます。ネストさせるとA∧B∧Cみたいなのを一気にdestructしたりできます。詳しくはリファレンスをどうぞ。
decompose [and or] H.
実はわたしは使ったこともちゃんと調べたこともないのですけど、賢く全部destructしつくしてくれる感じのtactic？
elim H
case H
destruct よりももっとプリミティブな操作です。destructすると「元々あった仮定を消して新しく分解後の仮定を追加」しますが、elim を使うと「元々の仮定は消さない。分解後の結果は過程に追加するのではなく、ゴールに->で追加」します。さらに、「分解した仮定Hが他の仮定の中に使われていた場合にそのHも書き換える」がdestructで書き換えないのがelim。まあなんだかややこしいのですが、要は、「destructはちょっとやり過ぎで困る」と思ったらelimに変えて試してみるといいかも…。
まあ、ややこしいことは気にせず仮定にInductiveなものがあったらとりあえずdestructしてみるという証明戦略は結構うまくいく気がします。

ややこしいことは気にせずといえば、カリーハワード対応脳の人には、destructのもっとずっとわかりやすい説明があります。要するにこれは、

Print De_Morgan2.

De_Morgan2 =
fun (A B : Prop) (H : (A -> False) /\ (B -> False)) (H0 : A \/ B) =>
match H with
| conj H1 H2 =>
    match H0 with
    | or_introl H3 => H1 H3
    | or_intror H3 => H2 H3
    end
end

パターンマッチなのです。

andとorとnot: コンストラクタ (2.3)

Coq

ここまでの内容をまとめると、

  • ゴールが A∧B の形なら ∧の公理(コンストラクタ)を使う
    • つまり apply conj.
  • ゴールが A∨B の形なら ∨の公理(コンストラクタ)を使う
    • つまり apply or_introl.
    • または apply or_intror.
    • どっちがいいかは人間が頑張って考える。

です。

これはこれでいいんですけど、「∧のコンストラクタの名前ってなんだったけ…」「∨のコンストラクタって…」って毎回思い出したり、リファレンス引いたりするのは面倒ですよね。

この辺は、自動化してくれる tactic があります。

Lemma De_Morgan:
  forall A B: Prop, ~(A \/ B) -> (~A /\ ~B).
Proof.
  unfold not.
  intros.
  constructor.  (* apply conj. の代わり *)

constructor. と打つと、名前忘れたけどコンストラクタ使うぜ！という意味になって、Coqさんが上手いことやってくれます。
orの場合はコンストラクタが2つあるので…

  intros.
  apply H.
  constructor 1. (* apply or_introl. の代わり *)
  exact H0.

  intros.
  apply H.
  constructor 2. (* apply or_intror. の代わり *)
  exact H0.
Qed.

どっちのコンストラクタなのか、「1番目のやつ！」「2番目のやつ！」と指定してあげましょう。番号指定しないと、コンストラクタを先頭から順にapplyしてみて成功した最初の結果を返すみたいです。

実は、さらにさらに、短く書く略記tacticも用意されています。

constructor.
ゴール命題の、コンストラクタをapply。(複数ある場合は最初にマッチした物)
constructor n.
ゴール命題の、n番目のコンストラクタをapply
split.
1つしかコンストラクタがないゴールに。そのコンストラクタをapply
left.
丁度2つコンストラクタがあるゴールに。constructor 1 と同じ
right.
丁度2つコンストラクタがあるゴールに。constructor 2 と同じ
splitは「"A∧B"を証明」というゴールを「Aを証明」と「Bを証明」に分ける(split)感覚で、leftは「"A∨B"を証明」というゴールを「Aを証明」に左(left)だけ残して変える感覚ですかね。rightは右。constructorのただの別名なので、splitもleftもrightも、andやor以外にも使えます（かえって意味がわかりにくくなったりするかもしれませんが…）。